Game theory is a mathematical and statistical framework designed to model strategic interactions among rational decision-makers. Whether in economics, politics, biology, or artificial intelligence, game theory helps explain and predict outcomes when multiple agents pursue conflicting or interdependent goals.
What is Game Theory?
At its core, game theory evaluates how participants—referred to as players—choose optimal strategies in response to the anticipated behavior of others. A game consists of players, strategies, and payoffs, all framed within a set of rules.
Common types include:
- Zero-sum games: One player’s gain equals another’s loss (e.g., chess, poker).
- Non-zero-sum games: Players may gain or lose simultaneously, making cooperation possible (e.g., trade negotiations).
- Cooperative vs. Non-cooperative games: In cooperative settings, players form binding agreements; in non-cooperative games, each player acts independently.
- Simultaneous vs. Sequential games: Depending on whether players act at the same time or in sequence, different strategies emerge.
Game theory assumes players are rational and seek to maximize their utility.
Mathematical Foundations
Game theory draws on linear algebra, combinatorics, and probability theory. One foundational concept is the Nash Equilibrium, where no player can benefit by changing their strategy unilaterally. In stochastic environments, Bayesian game theory incorporates uncertainty and belief updates, enabling analysis of games with incomplete information.
\[\text{Nash Equilibrium: } \forall i, \, u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*)\]Where:
\[s_i^* \text{ is the optimal strategy for player } i, \ \\ s_{-i}^* \text{ denotes the strategies of all other players}, \ and \ \\ u_i \text{ is the utility function for player } i \\\]Applications Across Disciplines
Game theory has practical value across fields:
- Economics: Oligopoly pricing, auction design, contract theory.
- Cybersecurity: Modeling attacker-defender interactions in threat environments.
- Biology: Explaining evolutionary strategies and cooperation among species.
- Artificial Intelligence: Multi-agent learning, adversarial training, negotiation systems.
- Public Policy: Analyzing voting systems, lobbying strategies, and conflict resolution.
“Game theory is the science of strategy, not just games.” — Avinash Dixit
Limitations and Real-World Use
While powerful, game theory has limitations. It assumes rational agents with complete information and perfect logical reasoning. Real-world decisions are often influenced by bounded rationality, emotions, and asymmetric information. Moreover, finding Nash equilibria in complex systems can be computationally intensive, leading to increased reliance on heuristics and simulations.
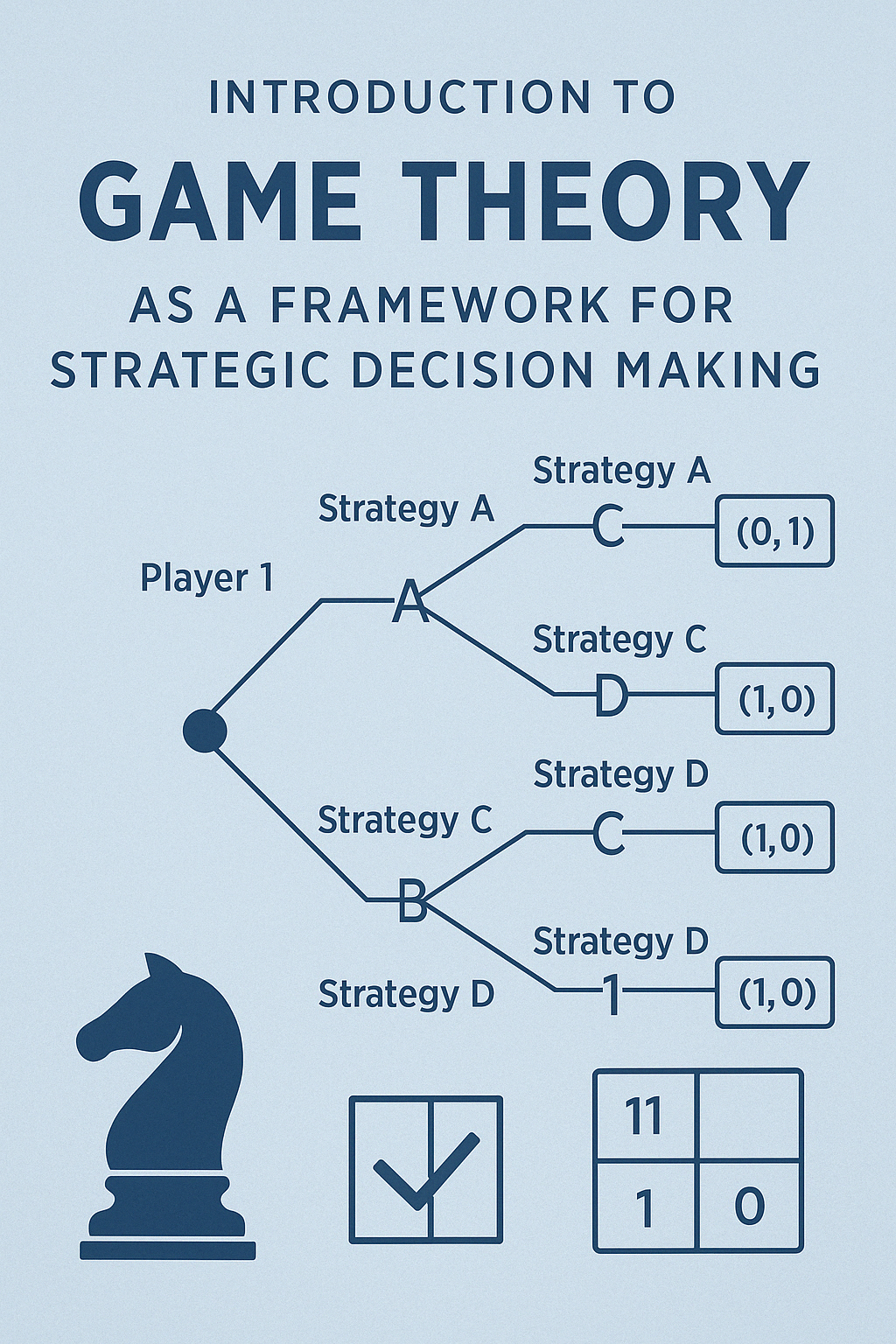Visualizing decision branches in a sequential game scenario.
Why It Matters
Understanding game theory empowers decision-makers to think critically about strategy. From business negotiations to military operations, it reveals not just what choices are possible, but why certain strategies dominate. As we move toward a more interconnected and data-driven world, the ability to model and respond to competitive environments will only grow in importance.
Final Thoughts
Game theory blends the precision of mathematics with the unpredictability of human behavior. It sharpens decision-making, challenges assumptions, and offers a structured lens for analyzing complex strategic situations. Whether you’re modeling adversarial threats, optimizing negotiation tactics, or designing market mechanisms, game theory equips you with the tools to think ahead—and think smart.
Game theory is not just theoretical—it’s an actionable framework with real-world implications.
